NumPy, SciPy and SciKits: Difference between revisions
No edit summary |
|||
| (41 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Python provides a framework on which numerical and scientific data processing can be built. As part of our [http://prancer.physics.louisville.edu/astrowiki/index.php/Python_for_Physics_and_Astronomy short course on Python for Physics and Astronomy] we will look at the capabilities of the [http://www.numpy.org NumPy], [http://www.scipy.org/ SciPy] and [http://scikits.appspot.com/scikits SciKits] packages. This is a brief overview with a few examples drawn primarily from the excellent but short introductory book ''SciPy and NumPy'' by [http://www.oreillynet.com/pub/au/4782 Eli Bressert (O'Reilly 2012)]. | Python provides a framework on which numerical and scientific data processing can be built. As part of our [http://prancer.physics.louisville.edu/astrowiki/index.php/Python_for_Physics_and_Astronomy short course on Python for Physics and Astronomy] we will look at the capabilities of the [http://www.numpy.org NumPy], [http://www.scipy.org/ SciPy] and [http://scikits.appspot.com/scikits SciKits] packages. This is a brief overview with a few examples drawn primarily from the excellent but short introductory book ''SciPy and NumPy'' by [http://www.oreillynet.com/pub/au/4782 Eli Bressert (O'Reilly 2012)]. The National Radio Astronomy Observatory's Common Astronomy Software site has a | ||
[http://casaguides.nrao.edu/index.php?title=NumpyBasics helpful introduction to NumPy]. | |||
== NumPy== | == NumPy== | ||
| Line 336: | Line 337: | ||
2x + y = 1 | 2x + y = 1 | ||
3y + z = 1 | 3y + z = 1 | ||
x + 4z = | x + 4z = 1 | ||
We would write | We would write | ||
| Line 459: | Line 460: | ||
[[File:Numpy_fft.png | center | 600 px]] | [[File:Numpy_fft.png | center | 600 px]] | ||
In practical applications it is desirable to have programs that will read files containing time or frequency data, perform the Fourier transform, and export a file with the transform from frequency to time, or from time to frequency. Two programs that are useful in this way are included in the [http://prancer.physics.louisville.edu/astrowiki/index.php/Python_examples examples] section. They depend on SciPy, which is described in the following. | |||
*fft_f2t.py | |||
*fft_t2f.py | |||
== SciPy and SciKits == | == SciPy and SciKits == | ||
| Line 472: | Line 477: | ||
For example, this program will create a set of test data of a | For example, this program will create a set of test data of a sparsely sampled cosine curve, and then fit it with a linear and a quadratic approximation. | ||
import numpy as np | import numpy as np | ||
| Line 484: | Line 489: | ||
y = np.cos(x) | y = np.cos(x) | ||
# Function to interpolate the data with a linear | # Function to interpolate the data with a linear interpolator | ||
f_linear = interp1d(x, y, kind='linear') | f_linear = interp1d(x, y, kind='linear') | ||
# Function to interpolate the data with a quadratic | # Function to interpolate the data with a quadratic interpolator | ||
f_quadratic = interp1d(x, y, kind='quadratic') | f_quadratic = interp1d(x, y, kind='quadratic') | ||
| Line 519: | Line 524: | ||
For 1-dimensional interpolation we have tried "linear" and "quadratic" which have clear meanings. The linear interpolation does a linear fit between two adjacent points and uses that to find the value at an x between those points. As you can see in the graph, the values follow a straight line connecting the sample points. The quadratic | For 1-dimensional interpolation we have tried "linear" and "quadratic" which have clear meanings. The linear interpolation does a linear fit between two adjacent points and uses that to find the value at an x between those points. As you can see in the graph, the values follow a straight line connecting the sample points. The quadratic interpolator takes points bracketing the x of interest and fits a quadratic polynomial to them. This allows the interpolation to have non-zero second derivative, and visually the new data will "curve" between the original sample points. | ||
The choices available for "kind" include | |||
*linear | |||
*quadratic | |||
*cubic | |||
*1,2,3, or higher indicating order of spline | |||
When the data support it, cubic interpolation introduces a third derivative, and gives a better representation of the original. You would not use linear interpolation of position to find velocity, and if you wanted to know the rate of change of acceleration you might use cubic interpolation. | |||
For more functions where the shape is not well represented by a polynomial, a spline fit will adapt to the available points and give a representation of the data better than fixed polynomials. The cubic spline is the most often used. Another implementation of spline fitting comes is incorporated into SciPy's UnivariateSpline function. | |||
Similar to the fitting above, the program to use spline fitting would have lines such as these | |||
from scipy.interpolate import UnivariateSpline | |||
# Generate sample xdata | |||
x = np.linspace(0,10.*np.pi,200) | |||
# Add noise to the sample y-data | |||
y = np.cos(x)+ 0.5 * np.random.normal(size=len(x)) | |||
# Function to interpolate the data with a univariate spline interpolator | |||
f_spline = UnivariateSpline(x, y, k=3, s=40) | |||
# Values of x for sampling inside the boundaries of the original data | |||
x_interpolated = np.linspace(x.min(),x.max(), 1000) | |||
# New values of y for these sample points | |||
y_interpolated_spline = f_spline(x_interpolated) | |||
The function call to UnivariateSpline uses an optional smoothing factor argument "s=40". If "s=0" the spline will interpolate through all the points. | |||
The larger this value, the more the spline filters short interval changes. Another optional argument is the order of the smoothing spline which is specified with "k=3". It must be less than or equal to 5. | |||
The complete program is in the Examples section. It will create a new data and a different fit on each run because it calls a random number generator. | |||
[[File:Interpolate_noisy.png | center | 600px ]] | |||
=== Integration === | === Integration === | ||
The SciPy ''integrate'' module supports numerical integrating a function of 1 to 3 variables, and integrating numerical data using trapezoidal, Simpson's rule, and Romberg methods. It also supports integrating ordinary differential equations. | |||
import scipy.integrate | |||
help("scipy.integrate") | |||
Integrating functions, given function object | |||
============================================ | |||
quad -- General purpose integration. | |||
dblquad -- General purpose double integration. | |||
tplquad -- General purpose triple integration. | |||
fixed_quad -- Integrate func(x) using [http://en.wikipedia.org/wiki/Gaussian_quadrature Gaussian quadrature] of order n. | |||
quadrature -- Integrate with given tolerance using Gaussian quadrature. | |||
romberg -- Integrate func using [http://en.wikipedia.org/wiki/Romberg%27s_method Romberg] integration. | |||
Integrating functions, given fixed samples | |||
========================================== | |||
trapz -- Use trapezoidal rule to compute integral from samples. | |||
cumtrapz -- Use trapezoidal rule to cumulatively compute integral. | |||
simps -- Use Simpson's rule to compute integral from samples. | |||
romb -- Use Romberg Integration to compute integral from | |||
-- (2**k + 1) evenly-spaced samples. | |||
As first example of integrating a function we will try a Lorentzian curve | |||
import numpy as np | |||
from scipy.integrate import quad | |||
import matplotlib.pyplot as plt | |||
# Define the integrand | |||
global a | |||
a = 10. | |||
f = lambda x: a**2 / (a**2 + x**2) | |||
x0 = -50. | |||
x1 = 50. | |||
integral, error = quad(f, x0, x1) | |||
# Compare integral to an area under the curve out to infinity | |||
area = a * np.pi | |||
print integral, area | |||
which we will plot in a moment. As is, it will print the integral from -50 to 50 under the Lorentzian curve (generated with the "f" definition) and a=10. As given, this Lorentzian has a peak of 1, and it falls to 0.5 of the peak at x=a. The area is exactly ''a x Pi''. | |||
You can iterate this by hand and see that as the limits are extended to infinity the integral slowly converges to the exactly value it would have at infinite limits. You can also generate a numerical infinity by using | |||
x0 = -np.inf | |||
x1 = np.ing | |||
A helpful plot can be made by adding this code: | |||
# Generate sample data | |||
x = np.linspace(-100,100.,200) | |||
y = f(x) | |||
# Create an integration region to show in the plot | |||
index01 = np.where( (x > x0) & (x < x1) ) | |||
y_region = y[index01] | |||
x_region = x[index01] | |||
# Create a plot with labeled axes | |||
plt.xlabel('X') | |||
plt.ylabel('F') | |||
plt.title('Sample Integration') | |||
plt.plot(x, y, color='blue', linestyle='-', marker='None', | |||
label='Lorentzian',linewidth=1.5) | |||
plt.fill_between(x_region, 0., y_region, color='gray') | |||
plt.legend() | |||
plt.minorticks_on() | |||
# Annotate with area | |||
area_label = 'Area: %f' % integral | |||
print area_label | |||
plt.annotate(area_label, xy= (.6,.6), xycoords='axes fraction', | |||
color='gray', fontsize=18) | |||
plt.show() | |||
With this you will see a graph of the function and the area being integrated. | |||
[[File:Integrate_function.png | center | 600px ]] | |||
Numerical integration would go similarly, except the input would be numpy arrays for x and y from data points or generated this way | |||
import numpy as np | |||
from scipy.integrate import trapz | |||
import matplotlib.pyplot as plt | |||
# Define the integrand | |||
global a | |||
a = 10. | |||
def f(x): | |||
value = a**2 / (a**2 + x**2) | |||
return value | |||
# For a good demonstration use | |||
x0 = -50. | |||
x1 = 50. | |||
x = np.linspace(x0,x1,1000) | |||
y = f(x) | |||
integral = trapz(y, x=x) | |||
=== Differentiation === | |||
SciPy provides differentiation of functions, much in the same fashion as it offers integration. | |||
derivative(func, x0, dx=1.0, n=1, args=(), order=3) | |||
where the "func" is the function being differentiated at "x0", "dx" is the interval on x used to find the derivative, "n" is order for the differentiation (by default 1 for first derivative), and "order" is the number of points to use in finding the derivative, not to be confused with the order of the differentiation. The "args" argument allows a function to call other arguments, rather than have them globally defined as we do in these examples. | |||
An example of its use to find the first derivative | |||
import numpy as np | |||
from scipy.misc import derivative | |||
# Define the function | |||
def f(x): | |||
value = x**2 * np.exp(-(x**2)) | |||
return value | |||
result = derivative(f, 1., dx=0.01) | |||
print result | |||
2.452186e-05 | |||
result = derivative(f, 2., dx=0.01) | |||
print result | |||
-0.21979 | |||
The result can be very sensitive to the choice of dx, which must be small enough to see the representative incremental changes. | |||
Differentiation of NumPy arrays can be done without additional programming, since it is only the difference between uniformly spaced values. However, for noisy data it would be best to interpolate the data first, and then take differences between adjacent points to calculate the derivative. Given the arrays, the derivative might be found with | |||
np.diff(y) / np.diff(x) | |||
with suitable tests for pathological behavior. | |||
In some cases it is possible to use symbolic analytic differentiation with the [http://sympy.org SymPy] package that has evolved into a robust full-featured symbolic mathematics tool. | |||
=== Statistics === | |||
As expected, SciPy provides statistical functions to Python in the form of various conventional statistical discrete and continuous distributions. The normal distribution is first one we would usually encounter: | |||
import numpy as np | |||
from scipy.stats import norm | |||
# Create a sample sapce | |||
x = np.linspace (-10,10,1000) | |||
# Set up the parameters of the distribution | |||
# Here loc makes it center on the origin and scale gives unit scaling | |||
dist = norm(loc=0, scale=1) | |||
# Now find the probability density function or pdf | |||
pdf = dist.pdf(x) | |||
# Plot the result ... | |||
[[File:Norm_probability.png | center | 600 px]] | |||
For the normal or Gaussian distribution, we would have | |||
N(x) = (1 / sigma sqr(2 pi) ) exp ( - (x - mu)^2 / 2 sigma^2 ) | |||
where sigma is the standard deviation, sigma^2 is the variance, and mu is the mean. | |||
The factor in front normalizes the distribution to unit area integrated to infinity on x. A Gaussian distribution centered at the origin has ''mu=0'' and a width such that at ''x=sqr(2)sigma'' the distribution is 1/e of its maximum at ''x=0''. | |||
Numpy would also allow creating a normal random array of values with mean 0 and variance 1, such as | |||
y = np.random.randn(1000) | |||
The mean, standard deviation, and variance could be assessed by evaluating the array | |||
mean = y.mean() | |||
std = y.std() | |||
var = y.var() | |||
=== SciKits Packages === | === SciKits Packages === | ||
We mention SciKits in the context of SciPy because it is a collection of SciPy applications that extend into many different domains of physics, astronomy, and engineering. The best introduction is to browse the [http://scikits.appspot.com/scikits SciKits website] and explore the variety there. In addition to image processing, you'll find speech processing, light scattering from non-spherical particles, sparse matrices, machine learning, vector field plotting, and more. Some are fully developed, others are works in progress. One of the most promising is the [http://scikits.appspot.com/cuda scikits.cuda] package, which interfaces Python to CUDA, NVidia's parallel processing through graphical processing units (GPU). The most recent hardware at this date (February 2017), is the | |||
the [http://www.nvidia.com/object/tesla-servers.html Tesla P100] Pascal architecture for servers, a supercomputer on a PCIe card with 3584 GPU cores, 9.3 Teraflops of single precision and 4.7 Teraflops of double precision processing power, and 16384 MB of memory. | |||
An example of a very useful Scikit is the [http://scikit-image.org/docs/dev/api/skimage.restoration.html image restoration package] which includes Lucy-Richardson deconvolution. A program that makes use of it for astronomical fits images is in the [http://prancer.physics.louisville.edu/classes/650/python/examples examples directory] of this site. Look for fits_lucy_richardson.py under the convolution examples. | |||
We will return to use other SciPy image processing routines later. | |||
== Examples == | == Examples == | ||
For examples of NumPy, see the [http://prancer.physics.louisville.edu/astrowiki/index.php/Python_examples examples] section. | For examples of NumPy and SciPy, see the [http://prancer.physics.louisville.edu/astrowiki/index.php/Python_examples examples] section. Look for | ||
*curve_fit_plot.example | |||
*integrate_function_plot.example | |||
*integrate_numerical_plot.example | |||
*interpolate_noisy_plot.example | |||
*interpolate_plot.example | |||
*norm_probability_plot.example | |||
*numpy_fft.example | |||
*fft_f2t.py | |||
*fft_t2f.py | |||
that contain most of the code shown in this section. | |||
Revision as of 04:47, 28 January 2017
Python provides a framework on which numerical and scientific data processing can be built. As part of our short course on Python for Physics and Astronomy we will look at the capabilities of the NumPy, SciPy and SciKits packages. This is a brief overview with a few examples drawn primarily from the excellent but short introductory book SciPy and NumPy by Eli Bressert (O'Reilly 2012). The National Radio Astronomy Observatory's Common Astronomy Software site has a helpful introduction to NumPy.
NumPy
NumPy adds arrays and linear algebra to Python, with special functions, transformations, the ability to operate on all elements of an array in one stroke. Remember that in addition to the web resources, in interactive Python try help() for more information on a function:
help("numpy.arange")
will tell you that arange takes one required argument but has several optional ones:
numpy.arange = arange(...) arange([start,] stop[, step,], dtype=None Return evenly spaced values within a given interval.
Let's see how to create and manipulate arrays with arange and other functions.
Arrays
Arrays are at the heart of NumPy. The program
import numpy as np mylist = [1, 3, 5, 7, 11, 13] myarray = np.array(mylist) print myarray
creates a list and makes an array from it. You can create an array of 30 32-bit floating point zeros with
myarray = np.zeros(30, dtype=np.float32)
The dtype argument is optional (defaults to float64) and can be
- unit8, 16, 32, 64
- int8, 16, 32, 64
- float16, 32, 64, 128
- complex64, 128
Arrays may also have character data, as in this
test = np.array(['a very','friendly','dog'])
which will be a dtype of
test.dtype
dtype('|S8')
meaning a string of 8 characters (set in this instance by the "friendly" element of the list). Arrays must have all elements the same size.
Arrays can be arranged to be multi-dimensional. In our example of zeros, we could instead have
myarray = np.zeros((3,4,5)) print myarray
which will show
array([[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]]])
Notice that the array is created with np.zeros(), and the argument is (3,4,5). This means an array of 3x4x5 elements, all zero (float64, by default), grouped as 3 elements, each of 4 elements, each of 5 elements.
An array can be reshaped after it is made. The array stays the same way in memory, but the grouping changes.
myarray = np.array( [1,3,5,7,11,13] )
makes a linear array of 6 elements, and
myarray.reshape(2,3)
changes its shape, so it will be
array([[ 1, 3, 5],
[ 7, 11, 13]])
To create an array of 1000 elements from 0 to 999, the function
my_1d_array = np.arange(1000)
It is reshaped into an array 10x10x10 with
my_3d_array = my_1d_array.reshape((10,10,10))
or an multi-dimensional array may be flattened
my_new_array = my_3d_array.ravel()
The original data remain unchanged, but they are sliced and indexed in different ways depending on the shape of the array and the choices for indexing it.
In summary, NumPy arrays may be created with
np.array() np.arange() np.zeros() np.empty()
reshaped with
myarray.reshape() myarray.ravel()
written to files in a binary format, and read back with
np.save('myfile.npy', myarray)
newarray = np.load('myfile.npy')
In the following we will see how to index within arrays, operate on arrays, and have arrays functionally combine with one another.
Indexing
Once an array is created, you can refer to it as a whole, or to its elements one-by-one. Create a list, turn it into an array, reshape it, and print it with something like this
#Make a list mylist = [1,2,3,4,5,6,7,8,9,10,11,12] #Make an array from a list myarray = np.array(mylist)
#Reshape the array my3by4 = myarray.reshape(3,4) print my3by4
to see
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
The (2,3) element in the reshaped array is
print my3by4[2][3]
12
Remember that indexing is from 0, so the "2" here means the 3 "group", and each group had 4 elements. The "3" means the fourth element of that group, which is 12.
Therefore, the notation is just like matrices, with the first index the row and the second index the column, enumerated from (0,0) at the upper left as printed.
Lists in Python are indexed similarly. Make a grouped list this way
alist = [[2,4],[6,8]] print alist[0][1]
displays
4
as expected. With NumPy you can also get access to a selected column --
arr = np.array(alist) print arr[0][1]
shows "4". The way to have column 1 alone is
print arr[:,1]
shows us a list of column 1,
[4 8]
and
print arr[1,:]
shows the list of row 1,
[6 8]
It's also possible to find elements conditionally. Let's make an array of 16 elements from 0 to 15, shape it to 4x4, and find those elements greater than 5
# Create the array myarray = np.arange(16).reshape(4,4) print myarray
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
# Index the array myindex = np.where(myarray <5) print(myindex)
(array([0, 0, 0, 0, 1]), array([0, 1, 2, 3, 0]))
mynewarray = myarray[myindex] print mynewarray
array([0, 1, 2, 3, 4])
Functions broadcasting over an array
The term broadcasting in NumPy refers to applying an operation to every element of an array. Consider this simple example
cube = np.zeros((2,2,2))
that makes a 2x2x2 cube of zeros. You can add 1 to every element, then divide them all by 3, with
newcube = (cube + 1.)/3. print newcube
array([[[ 0.33333333, 0.33333333],
[ 0.33333333, 0.33333333]],
[[ 0.33333333, 0.33333333],
[ 0.33333333, 0.33333333]]])
Perhaps more interestingly, create an array of multiples of Pi with
manypi = np.arange(8)*np.pi/4.
and then find the sine of these angles
manysines = np.sin(manypi)
The first one will produce the array of angles
array([ 0. , 0.78539816, 1.57079633, 2.35619449, 3.14159265,
3.92699082, 4.71238898, 5.49778714])
and the second will give the array of their sines
array([ 0.00000000e+00, 7.07106781e-01, 1.00000000e+00,
7.07106781e-01, 1.22464680e-16, -7.07106781e-01,
-1.00000000e+00, -7.07106781e-01])
NumPy math has the usual trigonometric functions, and others. A full list is in the documentation, and some useful ones are for element-by-element
- add(x1,x2)
- sub(x1,x2)
- multiply(x1,x2)
- divide(x1,x2)
- power(x1,x2)
- square(x)
- sqrt(x)
- exp(x)
- log(x)
- log10(x)
- absolute(x)
- negative(x)
- sin(x), cos(x), tan(x)
- arcsin(x), arccos(x), arctan(x)
- arctan2(x,y) returns the angle whose tangent is the ratio of x and y
- sinh(x), cosh(x), tanh(x)
- arcsinh(x), arccosh(x), arctanh(x)
- degrees(x) or rad2deg(x) convert from radians
- radians(x) or deg2rad(x) convert from degrees
- rint(x) round to the nearest integer
- fix(x) round to the nearest integer toward zero
The broadcast feature of NumPy arrays can be combined with selective indexing in an interesting way. Consider this program to make an array of random numbers in a Gaussian distribution with mean 0, and sigma 1
a = np.random.randn(100)
Print this will show 100 values, some negative, some positive. We can select only those larger than a cutoff, work with them, and put them back in the array
index = a > 0.75 b = a[index] b= b ** 3 - 100. a[index] = b
Printing index will show an array of True and False that mask the original array. The array b will only have those elements that satisified the condition used to make the index. The index is used again, to put modified elements back into the original array.
Matrix and vector math in NumPy
We have seen that NumPy has its own set of math functions that broadcast over arrays. If you define an array
a = np.arange(0,1,0.01)*np.pi
you will have an array from 0 to Pi in steps of 0.01*Pi. You can operate on this array, element by element, with np.cos
b = np.cos(a)
and have a new array that contains the cosine of each element of the first one.
Before we move on to SciPy, which builds on NumPy to add a number of useful features, there are two things we should note.
First, NumPy includes matrix math, either by mapping its native arrives to conventional matrices, or by invoking matrix math operations on its arrays. We will only look at this second way, which handles most applications and creates very clear code.
The product of two matrices is done with the "dot" operation between two NumPy arrays.
a = np.array(([1,2],[3,4])) b = np.array(([0,1],[1,0]))
makes two arrays that may be thought of as 2x2 matrices. To multiply them in the usual sense of matrix multiplication,
c = a.dot(b)
gives
array([[2, 1],
[4, 3]])
and
d = b.dot(a)
gives
array([[3, 4],
[1, 2]])
A matrix inverse is found in the linalg package of NumPy
e = np.linalg.inv(a)
With this we can solve linear equations. Suppose that you have the system of 3 equations in 3 unknowns:
2x + y = 1 3y + z = 1 x + 4z = 1
We would write
a = np.array([[2, 1, 0], [0, 3, 1], [1, 0, 4]]) b = np.array([[1],[1],[1]])
The linear algebra formulation is a.X = b, with solution X = a^-1 . b where a^-1 is the inverse of a. In NumPy we would find
x = np.linalg.inv(a).dot(b) print x
which as a program returns the solution
array([[ 0.36],
[ 0.28],
[ 0.16]])
NumPy also supports vector math with np.cross. For example if
a = [1, 1, 0] b = [0, 0, 1] c = np.cross(a, b) print c array([ 1, -1, 0])
d = np.dot(a, b) print d
0
Or, to illustrate the dot product in another example
a = np.array([1,0,0]) b = np.array([2,1,3]) d = np.dot(a,b) print d
2
For 1-D vectors this is the same as the inner product
d = np.inner(a,b) print d
2
Fourier Transforms in NumPy
NumPy provides Fourier Transforms in several functions, including the one-dimension discrete Fast Fourier Transform or FFT with the function fft(a), and the one-dimensional FFT of real data with rfft(a). It also has n-dimensional Fourier Transforms as well.
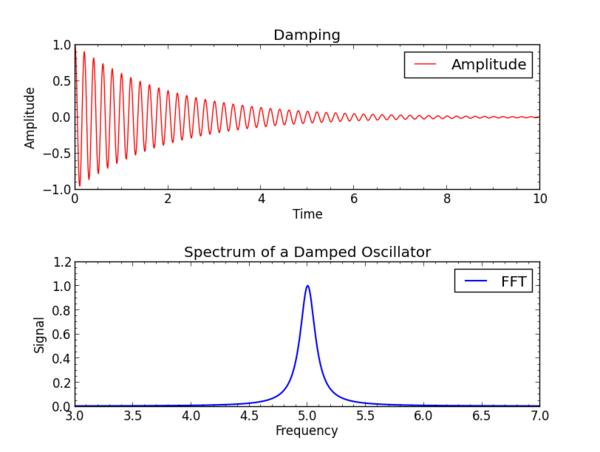
As a very simple example, let's consider an exponential decay modulating a sine wave adapted from our dampled cosine plotting example to use NumPy arrays:
# Import the plotting and math packages import matplotlib.pyplot as plt import numpy as np
# Define initial constants f0 = 5. a0 = 100. tdecay = 2. timestep = 0.01 timemax = 100.
time = np.arange(0,timemax,timestep) amplitude = np.exp(-time/tdecay)*np.cos(2.*np.pi*f0*time)
With NumPy we do not have to loop to calculate each point of the damped oscillator's path.
Now we add a Fourier Transform with lines
# Use an FFT to calculate its spectrum spectrum = np.fft.fft(amplitude) # Find the positive frequencies frequency = np.fft.fftfreq( spectrum.size, d = timestep ) index = np.where(frequency >= 0.) # Scale the real part of the FFT and clip the data clipped_spectrum = timestep*spectrum[index].real clipped_frequency = frequency[index]
The array "spectrum" has the spectrum of the original data, and "frequency" has the corresponding frequencies. We clip the negative frequencies.
# Create a figure fig = plt.figure()
# Adjust white space between plots fig.subplots_adjust(hspace=0.5)
# Create x-y plots of the amplitude and transform with labeled axes
data1 = fig.add_subplot(2,1,1)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Damping')
data1.plot(time,amplitude, color='red', label='Amplitude')
plt.legend()
plt.minorticks_on()
plt.xlim(0., 10.)
data2 = fig.add_subplot(2,1,2)
plt.xlabel('Frequency')
plt.ylabel('Signal')
plt.title('Spectrum of a Damped Oscillator')
data2.plot(clipped_frequency,clipped_spectrum, color='blue', linestyle='solid',
marker='None', label='FFT', linewidth=1.5)
plt.legend()
plt.minorticks_on()
plt.xlim(3., 7.)
# Show the data plt.show()
This will make an interactive plot that looks like this
In practical applications it is desirable to have programs that will read files containing time or frequency data, perform the Fourier transform, and export a file with the transform from frequency to time, or from time to frequency. Two programs that are useful in this way are included in the examples section. They depend on SciPy, which is described in the following.
- fft_f2t.py
- fft_t2f.py
SciPy and SciKits
NumPy adds numerical support to Python that enables a broad range of applications in science in engineering. SciPy and SciKits use NumPy to provide features that are targeted at scientific computing. These packages are dynamic, with community support that is adding new contributions and updating older ones. As we continue our short course on Python for Physics and Astronomy we will explore a few of these to see how we can use Python for interpolating data, numerical integration, and image processing. A reference guide to SciPy is available on line from the their website, or in this reference pdf if that site is not available.
Interpolation
Frequently we will have data that are not as finely spaced as we would like, but which are smooth enough to reliably interpolate between the known points. An example might be a resource-intensive computation of a wavefunction for a complex system, a model of the opacity of stellar atmosphere, or a calculation of of a planetary atmosphere on a coarse spatial grid. You can also interpolate noisy data and recover an acceptable estimate of the values between the sampled points.
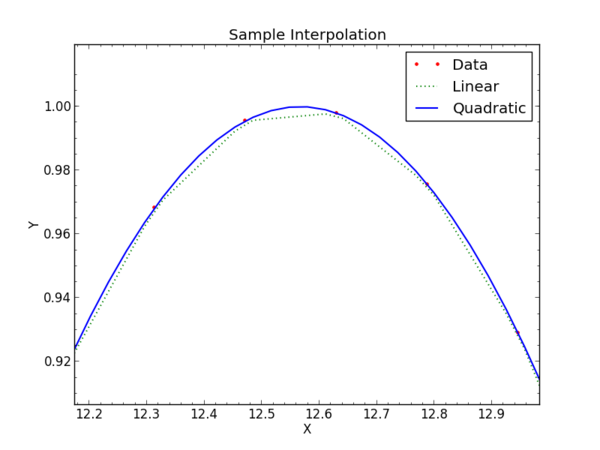
For example, this program will create a set of test data of a sparsely sampled cosine curve, and then fit it with a linear and a quadratic approximation.
import numpy as np from scipy.interpolate import interp1d import matplotlib.pyplot as plt
# Import your data into a np array yn for x or ...
# Generate sample data x = np.linspace(0,10.*np.pi,200) y = np.cos(x)
# Function to interpolate the data with a linear interpolator f_linear = interp1d(x, y, kind='linear')
# Function to interpolate the data with a quadratic interpolator f_quadratic = interp1d(x, y, kind='quadratic')
# Values of x for sampling inside the boundaries of the original data x_interpolated = np.linspace(x.min(),x.max(), 1000)
# New values of y for these sample points y_interpolated_linear = f_linear(x_interpolated) y_interpolated_quadratic = f_quadratic(x_interpolated)
It helps to plot this
# Create an plot with labeled axes
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Sample Interpolation')
plt.plot(x, y, color='red', linestyle='None',
marker='.', markersize=10., label='Data')
plt.plot(x_interpolated, y_interpolated_linear, color='green', linestyle=':',
marker='None', label='Linear', linewidth=1.5)
plt.plot(x_interpolated, y_interpolated_quadratic, color='blue', linestyle='-',
marker='None', label='Quadratic', linewidth=1.5)
plt.legend()
plt.minorticks_on()
plt.show()
The result, zoomed in to see a few points in detail, looks like this on an interactive screen:
For 1-dimensional interpolation we have tried "linear" and "quadratic" which have clear meanings. The linear interpolation does a linear fit between two adjacent points and uses that to find the value at an x between those points. As you can see in the graph, the values follow a straight line connecting the sample points. The quadratic interpolator takes points bracketing the x of interest and fits a quadratic polynomial to them. This allows the interpolation to have non-zero second derivative, and visually the new data will "curve" between the original sample points.
The choices available for "kind" include
- linear
- quadratic
- cubic
- 1,2,3, or higher indicating order of spline
When the data support it, cubic interpolation introduces a third derivative, and gives a better representation of the original. You would not use linear interpolation of position to find velocity, and if you wanted to know the rate of change of acceleration you might use cubic interpolation.
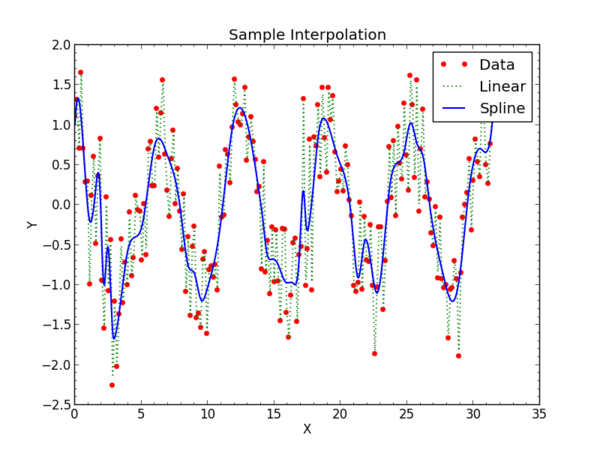
For more functions where the shape is not well represented by a polynomial, a spline fit will adapt to the available points and give a representation of the data better than fixed polynomials. The cubic spline is the most often used. Another implementation of spline fitting comes is incorporated into SciPy's UnivariateSpline function.
Similar to the fitting above, the program to use spline fitting would have lines such as these
from scipy.interpolate import UnivariateSpline
# Generate sample xdata x = np.linspace(0,10.*np.pi,200)
# Add noise to the sample y-data y = np.cos(x)+ 0.5 * np.random.normal(size=len(x))
# Function to interpolate the data with a univariate spline interpolator f_spline = UnivariateSpline(x, y, k=3, s=40)
# Values of x for sampling inside the boundaries of the original data x_interpolated = np.linspace(x.min(),x.max(), 1000)
# New values of y for these sample points y_interpolated_spline = f_spline(x_interpolated)
The function call to UnivariateSpline uses an optional smoothing factor argument "s=40". If "s=0" the spline will interpolate through all the points.
The larger this value, the more the spline filters short interval changes. Another optional argument is the order of the smoothing spline which is specified with "k=3". It must be less than or equal to 5.
The complete program is in the Examples section. It will create a new data and a different fit on each run because it calls a random number generator.
Integration
The SciPy integrate module supports numerical integrating a function of 1 to 3 variables, and integrating numerical data using trapezoidal, Simpson's rule, and Romberg methods. It also supports integrating ordinary differential equations.
import scipy.integrate
help("scipy.integrate")
Integrating functions, given function object
============================================
quad -- General purpose integration.
dblquad -- General purpose double integration.
tplquad -- General purpose triple integration.
fixed_quad -- Integrate func(x) using Gaussian quadrature of order n.
quadrature -- Integrate with given tolerance using Gaussian quadrature.
romberg -- Integrate func using Romberg integration.
Integrating functions, given fixed samples
==========================================
trapz -- Use trapezoidal rule to compute integral from samples.
cumtrapz -- Use trapezoidal rule to cumulatively compute integral.
simps -- Use Simpson's rule to compute integral from samples.
romb -- Use Romberg Integration to compute integral from
-- (2**k + 1) evenly-spaced samples.
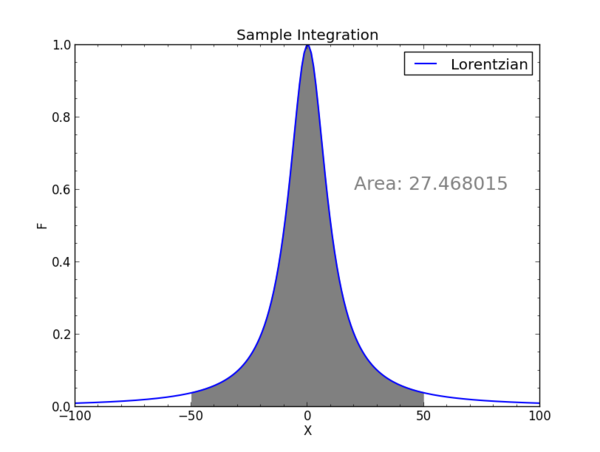
As first example of integrating a function we will try a Lorentzian curve
import numpy as np from scipy.integrate import quad import matplotlib.pyplot as plt
# Define the integrand
global a a = 10. f = lambda x: a**2 / (a**2 + x**2)
x0 = -50. x1 = 50.
integral, error = quad(f, x0, x1)
# Compare integral to an area under the curve out to infinity
area = a * np.pi print integral, area
which we will plot in a moment. As is, it will print the integral from -50 to 50 under the Lorentzian curve (generated with the "f" definition) and a=10. As given, this Lorentzian has a peak of 1, and it falls to 0.5 of the peak at x=a. The area is exactly a x Pi.
You can iterate this by hand and see that as the limits are extended to infinity the integral slowly converges to the exactly value it would have at infinite limits. You can also generate a numerical infinity by using
x0 = -np.inf x1 = np.ing
A helpful plot can be made by adding this code:
# Generate sample data x = np.linspace(-100,100.,200) y = f(x)
# Create an integration region to show in the plot index01 = np.where( (x > x0) & (x < x1) ) y_region = y[index01] x_region = x[index01]
# Create a plot with labeled axes
plt.xlabel('X')
plt.ylabel('F')
plt.title('Sample Integration')
plt.plot(x, y, color='blue', linestyle='-', marker='None',
label='Lorentzian',linewidth=1.5)
plt.fill_between(x_region, 0., y_region, color='gray')
plt.legend()
plt.minorticks_on()
# Annotate with area area_label = 'Area: %f' % integral print area_label plt.annotate(area_label, xy= (.6,.6), xycoords='axes fraction', color='gray', fontsize=18) plt.show()
With this you will see a graph of the function and the area being integrated.
Numerical integration would go similarly, except the input would be numpy arrays for x and y from data points or generated this way
import numpy as np from scipy.integrate import trapz import matplotlib.pyplot as plt
# Define the integrand
global a a = 10.
def f(x): value = a**2 / (a**2 + x**2) return value
# For a good demonstration use x0 = -50. x1 = 50.
x = np.linspace(x0,x1,1000) y = f(x)
integral = trapz(y, x=x)
Differentiation
SciPy provides differentiation of functions, much in the same fashion as it offers integration.
derivative(func, x0, dx=1.0, n=1, args=(), order=3)
where the "func" is the function being differentiated at "x0", "dx" is the interval on x used to find the derivative, "n" is order for the differentiation (by default 1 for first derivative), and "order" is the number of points to use in finding the derivative, not to be confused with the order of the differentiation. The "args" argument allows a function to call other arguments, rather than have them globally defined as we do in these examples.
An example of its use to find the first derivative
import numpy as np from scipy.misc import derivative
# Define the function def f(x): value = x**2 * np.exp(-(x**2)) return value
result = derivative(f, 1., dx=0.01) print result 2.452186e-05
result = derivative(f, 2., dx=0.01) print result -0.21979
The result can be very sensitive to the choice of dx, which must be small enough to see the representative incremental changes.
Differentiation of NumPy arrays can be done without additional programming, since it is only the difference between uniformly spaced values. However, for noisy data it would be best to interpolate the data first, and then take differences between adjacent points to calculate the derivative. Given the arrays, the derivative might be found with
np.diff(y) / np.diff(x)
with suitable tests for pathological behavior.
In some cases it is possible to use symbolic analytic differentiation with the SymPy package that has evolved into a robust full-featured symbolic mathematics tool.
Statistics
As expected, SciPy provides statistical functions to Python in the form of various conventional statistical discrete and continuous distributions. The normal distribution is first one we would usually encounter:
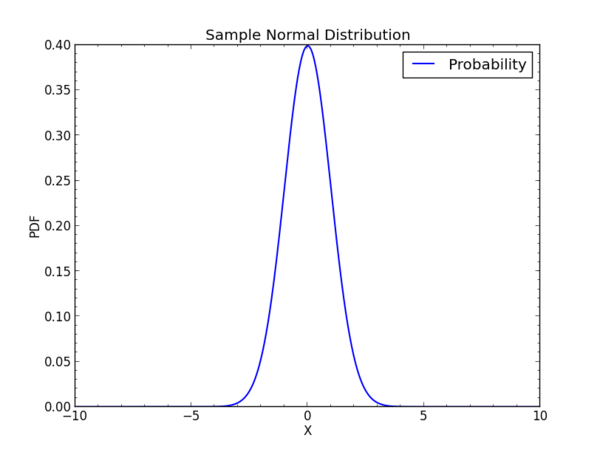
import numpy as np from scipy.stats import norm # Create a sample sapce x = np.linspace (-10,10,1000) # Set up the parameters of the distribution # Here loc makes it center on the origin and scale gives unit scaling dist = norm(loc=0, scale=1) # Now find the probability density function or pdf pdf = dist.pdf(x)
# Plot the result ...
For the normal or Gaussian distribution, we would have
N(x) = (1 / sigma sqr(2 pi) ) exp ( - (x - mu)^2 / 2 sigma^2 )
where sigma is the standard deviation, sigma^2 is the variance, and mu is the mean. The factor in front normalizes the distribution to unit area integrated to infinity on x. A Gaussian distribution centered at the origin has mu=0 and a width such that at x=sqr(2)sigma the distribution is 1/e of its maximum at x=0.
Numpy would also allow creating a normal random array of values with mean 0 and variance 1, such as
y = np.random.randn(1000)
The mean, standard deviation, and variance could be assessed by evaluating the array
mean = y.mean() std = y.std() var = y.var()
SciKits Packages
We mention SciKits in the context of SciPy because it is a collection of SciPy applications that extend into many different domains of physics, astronomy, and engineering. The best introduction is to browse the SciKits website and explore the variety there. In addition to image processing, you'll find speech processing, light scattering from non-spherical particles, sparse matrices, machine learning, vector field plotting, and more. Some are fully developed, others are works in progress. One of the most promising is the scikits.cuda package, which interfaces Python to CUDA, NVidia's parallel processing through graphical processing units (GPU). The most recent hardware at this date (February 2017), is the the Tesla P100 Pascal architecture for servers, a supercomputer on a PCIe card with 3584 GPU cores, 9.3 Teraflops of single precision and 4.7 Teraflops of double precision processing power, and 16384 MB of memory.
An example of a very useful Scikit is the image restoration package which includes Lucy-Richardson deconvolution. A program that makes use of it for astronomical fits images is in the examples directory of this site. Look for fits_lucy_richardson.py under the convolution examples.
We will return to use other SciPy image processing routines later.
Examples
For examples of NumPy and SciPy, see the examples section. Look for
- curve_fit_plot.example
- integrate_function_plot.example
- integrate_numerical_plot.example
- interpolate_noisy_plot.example
- interpolate_plot.example
- norm_probability_plot.example
- numpy_fft.example
- fft_f2t.py
- fft_t2f.py
that contain most of the code shown in this section.
Assignments
For the assigned homework to use these ideas, see the assignments section.