How to Measure Distances in the Universe: Difference between revisions
| Line 113: | Line 113: | ||
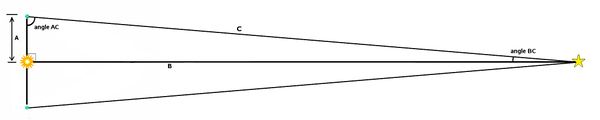
<center>Parallax measures the shift in the angle between a given star and very distant ones to obtain the small angle of triangulation</center> | <center>Parallax measures the shift in the angle between a given star and very distant ones to obtain the small angle of triangulation</center> | ||
Since the sky is a great hemisphere, we can think of it in degrees, the horizon being 0 and overhead being 90 degrees up. Each little degree may be divided into 60 tiny arcminutes. Each arcminute may be divided into 60 even smaller arcseconds. If a star shifts one arcsecond when the Earth moves one astronomical unit through space, its angle of parallax is one arcsecond, and the star is one parsec distant, about 3.26 light years away. | Since the sky is a great hemisphere, we can think of it in degrees, the horizon being 0 and overhead being 90 degrees up. Each little degree may be divided into 60 tiny arcminutes. Each arcminute may be divided into 60 even smaller arcseconds. If a star shifts one arcsecond when the Earth moves one astronomical unit through space, its angle of parallax is one arcsecond, and the star is one parsec distant, about 3.26 light years away. | ||
| Line 180: | Line 181: | ||
<center>Proxima Centauri, the nearest star to Earth, about 4.3 light years away</center> | <center>Proxima Centauri, the nearest star to Earth, about 4.3 light years away</center> | ||
== Inverse Square == | == Inverse Square == | ||
Revision as of 03:59, 6 March 2012
Lasers
Distances to the Moon are measured by timing a pulse of laser light reflected from mirrors placed on the surface by Apollo astronauts in the 1960's and 1970's. A laser pulse travels 400,000 kilometers from the Earth to the Moon in 1.3 seconds. Send the pulse out, and 2.6 second later it comes back to you.
Distances to Sun and planets are measured by timing radio signals from man-made satellites orbiting around those planets. The images of Saturn returned by the Cassini satellite take about 1 hour and 23 minutes to travel 1,300,000,000 kilometers to reach us.
Within the solar system we measure distances by comparison to the Earth-Sun distance, and use the Astronomical Unit as the measuring stick. Since the Earth's orbit is an ellipse, astronomers prefer to define the "AU" for an imaginary planet that would orbit in the Sun in a circle in the same time it takes for Earth to orbit in its ellipse. For most purposes this means that the AU is the average distance from the Earth to the Sun. It is precisely
1 Astronomical Unit = 149,597,871.5 kilometers
or about 150 million km, 93 million miles, 8.3 light minutes.
Triangulation
Triangulation has been used to measure distances for thousands of years. Greek astronomers used it to try to determine distances of the Moon and Sun. Kepler used it to find distances to the planets. Surveyors use it to locate to locate property boundaries and plan construction. You could use it for something as simple as finding the height of a telephone pole without climbing it, tape measure in hand.
A simple example in astronomy occurs when we measure the direction to an object seen when the Earth is first on one side of its orbit, and then again six months later when Earth is on the other side.
It's easy to see from this figure that the size of the angles tells us the distance B since we know that A, one astronomical unit, is 150,000,000 km. Let's call the angle to the object AC, and agree to measure it from the direction to the Sun.
The triangle with the sides A, B, and C is a "right" triangle. That's one that has a "right" or 90 degree angle. The right angle is marked in the figure; it's the one that is at the Sun.
In a right triangle, the tangent of an angle is the ratio of the side opposite the angle to the side next to the angle. In this case, we'd say
Tangent of the angle AC = B/A
If you know the angle, and can calculate its tangent, then the distance B is simply
B = A x Tangent of the angle AC
In the solar system "A" is the distance from Earth to the Sun, the astronomical unit, 150,000,000 km or 93,000,000 miles.
Suppose you see a mystery object like this one, and you want to learn where and what it is. You can see how big it appears to be, but since you do not know its distance, you cannot tell how big it really is.
You measure angle AC to be 89 degrees. Type 89 into your calculator and press tan to find that the tangent of angle 89 degrees is 57.3. "A" in our equation is just 1 astronomical unit:
Distance = A x tan(89)
Distance = 1 x 57.3 astronomical units
The greater the angle, the more distant the object. This mystery object is 57.3 AU away, somewhere in the vicinity of the Kuiper Belt.
Would you rather know how far it is in kilometers? The astronomical unit "A" is 150,000,000 km, and our object is at
Distance = 150,000,000 x tan(89) kiolmeters
Distance = 150,000,000 x 57.3
Distance = 8,593,494,245 kilometers
By the way, since light travels 300,000 kilometers per second, it takes
8,593,494,245 /300,000 = 28,644 seconds
to reach us. That's nearly 8 hours!
Parallax
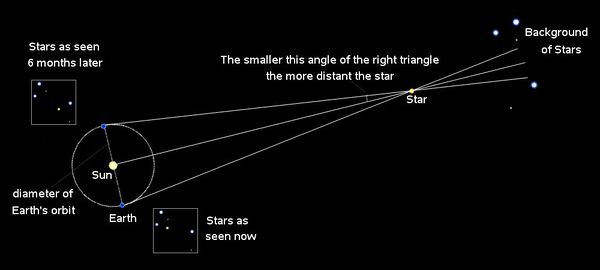
Parallax is the same as triangulation. We measure how much the direction to a distant object changes when it is observed from opposite sides of Earth's orbit. Distant stars provide a background for measuring the closer ones.
When out on an evening's stroll, and a nearby tree seems to go by quickly as we walk, while the distant Moon seems to stand still overhead, we're experiencing parallax. When Earth moves from one side of the Sun to the other, a nearby star will appear to shift against the background of distant stars. The greater the shift, the closer the star.
Since the sky is a great hemisphere, we can think of it in degrees, the horizon being 0 and overhead being 90 degrees up. Each little degree may be divided into 60 tiny arcminutes. Each arcminute may be divided into 60 even smaller arcseconds. If a star shifts one arcsecond when the Earth moves one astronomical unit through space, its angle of parallax is one arcsecond, and the star is one parsec distant, about 3.26 light years away.
One second of arc is a very small angle. Imagine a quarter held up in front of you at arm's length. That's about 1 degree across. Now take that quarter 4 kilometers or about 2.5 miles away. It's one arcsecond across.
Example: Suppose we see a small red star and we want to know how distant it is.
This time we use angle BC in the figure. The parallax that we measure from Earth is the same as the angle one astronomical unit would be if seen from the star. Just as before, the tangent is the ratio of the side opposite the angle to the side near it in this right triangle:
tangent of the angle BC = A/B
B = A / tan(BC)
The angles we measure for stars are very, very small. That makes the math very simple, because for a very small angle in arcseconds
tan(BC) = BC/206265
B = A x 206265 / BC
It's easy now. A is one astronomical unit, the distance from Earth to the Sun. If BC is one arcsecond, the star is 1 x 206,265 astronomical units away. That's one parsec, 3.26 light years. The smaller the parallax, the greater the distance:
Distance in parsecs = 1 / Parallax in arcseconds
What if this small red mystery star had a parallax of 0.75 arcseconds? It's distance would be
Distance = 1/ 0.75 = 1.33 parsecs
Distance =1.33 x 3.26 = 4.3 light years
The only star this nearby is Proxima Centauri, the nearest star to us beyond the Sun. It's visible only with a good telescope from the southern hemisphere, a non-descript red dot among hundreds of thousands of other stars in the sky. When we see this star at night, we are seeing it as it was 4.3 years ago because the light took that long to reach us. It is set apart from all the others by having the largest parallax of any star. Because it is so close, its motion relative to the Sun in our galaxy carries it past us at an unusually fast clip. Year to year it moves across the sky with the combined back and forth motion of its parallax, and the steady drift of its proper motion through the galaxy.
Inverse Square
Once the brightness of a specific type of star is known close up, we can tell the distance of similar stars by how much fainter they appear when farther away. The rule that applies is the Inverse Square Law.
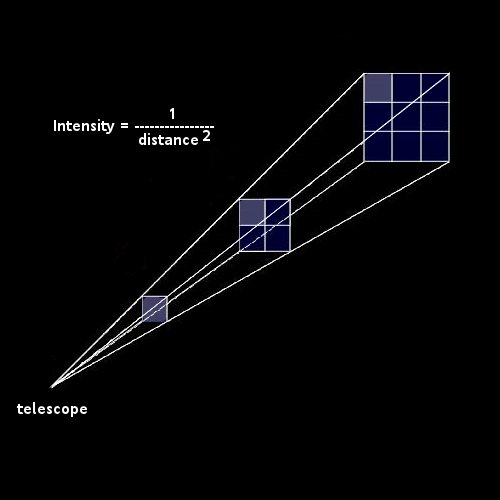
If at a certain distance the brightness of a star is known, then at twice the distance it will only be 1/4th as bright in a telescope. At three times the distance the brightness will be only 1/9th. Conversely, if a star of known brightness appears 1/4th as bright as one at a known distance, the star must be twice as far away. If a star appears 1/9th as bright, it must be 3 times the distance of the original star. Your eye senses this as "brightness". An astronomer counts the number of photons of light from the star her telescope captures each second.
The more distant a star, the more area its light is spread over when it arrives at our telescope, and the fainter it appears to be.
An Example
Suppose we see a Type Ia supernova in a galaxy 1,000,000 ly away. Then we see another Type Ia supernova in another galaxy, only this time it appears only 1/4th as bright as the first one. How far is the second galaxy?
The inverse square law says that the intensity falls as the square of the distance. For the second galaxy compared to the first:
Intensity = 1 / (Distance)2
1 /4 = 1 / (Distance)2
Distance = 2
2 x 1,000,000 ly = 2,000,000 ly
The second galaxy is twice as distant as the first. It would be 2,000,000 ly away.
More Examples
Suppose the Type Ia supernova were 1/9th as bright. It would be 3 times more distant.
If the supernova were 1/16th as bright it would be 4 times more distant.
If the Type Ia supernova were 1/10,000th as bright it would be 100 times more distant, 100,000,000 ly away.
If the Type Ia supernova were 1/127690000th as bright it would be 11300 times more distant! If it were 11,300 times more distant than 1,000,000 ly away, it would be 11,300,000,000 ly years away ...11.3 billion light years away !!!
The oldest and most distant Type Ia supernova ever seen is SN 1997 11.3 billion ly away !!!
Distance to the Magellanic Clouds
Once we knew the brightness and distance for different types of stars within our Milky Way galaxy, and we had ways to identify the type of star they were, we could measure the distance to the nearby Magellanic Clouds using the inverse square method:
- Identify a star of the same type as a nearby one at a known disance.
- Compare their brightnesses.
- Calculate the distance to the Magellanic Cloud using the Inverse Square Law.
The normal stars that were found in the Magellanic Clouds were too faint, however, to be used in galaxies at even greater distances.
Cepheid Variables
Over 80 years ago, Henrietta Leavitt worked at Harvard College Observatory measuring photographs of Cepheid variable stars in the Small Magellanic Cloud, a compact galaxy that is a nearby companion to our Milky Way.
These stars are similar to one that is relatively nearby, and that appears in the constellation of Cepheus. They are variable, increasing, decreasing, and increasing in brightness again. Some of them may go through a cycle in less than a day. Others may take weeks. Henreitta Leavitt was trying to make sense of the variations.
She found that the Cepheid's actual brightness could be predicted by their period, the time it takes for them to go through a cycle of change. This is called the Period-Luminosity Relationship. It's a seemingly mundane detail of the properties of these aging, pulsing, stars. Yet, it holds a key to finding the distances to galaxies. These stars are so bright, and their variations so distinctive, that we can pick them out of the crowd. The period of their variation tells us how bright they really are. It is just like reading the wattage on a lightbulb.
For instance, those blinking once every 3 days were about 800 times the brightness of the Sun, whereas those blinking slower, once in 30 days, were 10,000 times the Sun's brightness.
With their brightnesses known, distances to galaxies in which they resided could be determined by using the inverse square method. Edwin Hubble found Cepheid variables in the Andromeda Galaxy, which place it 2.5 million light years away. It's the most distant object you can see in the sky without a telescope. The light that made this image left the galaxy 2.5 million years ago.
Because of photography, and the high average brightness of Cepheid variable stars, distances to galaxies as far as 60 million light years away (such as those in the Virgo Cluster of galaxies shown below) could be measured.
Type Ia Supernovae
Small stars, those without enough mass to cause a supernova explosion, become white dwarfs. Occasionally a white dwarf will gather mass from a nearby companion star, reach the Chandrasekhar Limit of 1.4 solar masses, explode, and be seen as a Type Ia supernova. Since all Type Ia Supernova have the same mass, they have the same brightness. If one appears dimmer, we know it is more distant. We need only apply the Inverse Square Law and we will know the distance to the galaxy in which it appears!
Even brighter than Cepheid variables, Type Ia Supernovae are as bright as a whole galaxy. They have been used to measure distances to galaxies as far as 11 billion light years away.
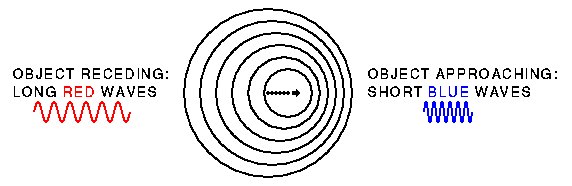
Redshifts
Train whistles sound lower pitched as they recede, due to the moving source of the sound waves. This is called the Doppler shift. Light waves from a galaxy that is moving away also appear longer in wavelength, lower in frequency, and therefore redder in color. This effect is called the redshift, and it provides a way for us to measure distances to galaxies.
Once Edwin Hubble had identified Cepheid variables in Andromeda galaxy, he could use the Period-Luminosity Relationship, discovered by Henrietta Levitt, to find the brightnesses of the stars. With that, and the inverse square law, he could measure the distance to the Andromeda galaxy, and to other galaxies in which Cepheid variables occurred.
Hubble noticed a pattern in this new data. He noticed the greater the distance of the galaxy, the greater its redshift. Almost all the galaxies he measured appeared to be moving away from us, and the greater the distance of the galaxy, the faster it was going. His original measurements have been replaced by others of more accuracy, and extended out much farther. The relationship he discovered is called the Hubble Law.
Cepheid variables are not bright enough to use for distance measurements much beyond the 60 million light years of the Virgo Cluster. The Type Ia supernovae are so much brighter that we can see them billions of light years away. The Hubble Law holds, even at these distances; even looking back billions of years into the past, it was found that the distance of a galaxy is proportional to its redshift.
Now the redshift could provide the distance to any galaxy. The more distant the galaxy the greater the redshift. Distance could be measured in redshifts. A cluster of galaxies with an average redshift z = 0.01 means the galaxies are moving away at about 0.01th the speed of light. If it is has a redshift z = 0.02 it is moving away at twice that speed, and is twice as far away.
Astronomers measure the wavelength of light by analyzing the spectrum of a star or even an entire galaxy. When we look at a distant receding galaxy we see all the wavelengths of its spectral features increased by the same factor, 1+z. When z is small it is approximately v/c where "v" is the speed of the galaxy moving away, and "c" is the speed of light. However, matter cannot travel travel faster than the speed of light, and at larger z the speeds just get closer and closer to "c". We will look at how this works in more detail in a later unit when we explore the effects of relativity. For now, remember that the most distant galaxies appear to recede from us at nearly the speed of light, and that the more distant they are, the more its spectral features are reddened, shifted to longer and longer wavelengths.
Not only could distances be measured, but since all distant galaxies are receding from us, and the more distant a galaxy, the faster the galaxy it goes, it appears that the universe is expanding!
Not only that, but if you follow their paths backwards, it seems that all galaxies would at some time have been in the same place, beginning at a singular event that we call the Big Bang!
By the end of next week you will be able easily to measure the size of the visible Universe, and to follow the of galaxies backwards in time to the beginning of the universe.
In all of human history only a few of the greatest thinkers have been able to do this, but you will find it easy!
Can you tell which galaxies are more distant? (Note exceptions: elliptical galaxies are redder by nature, and galaxies come in a range of sizes and types.)