The globular cluster M15 is very bright, but compact. At a distance
of about 33,600 light years it takes a long exposure to capture its
faintest stars. This image is a relatively short exposure. It is limited by
the brightness of the night sky at our site, by ``seeing'' or atmospheric
turbulence, and by the ``less than perfect''
focus (which smears the otherwise point image of a star over several pixels).
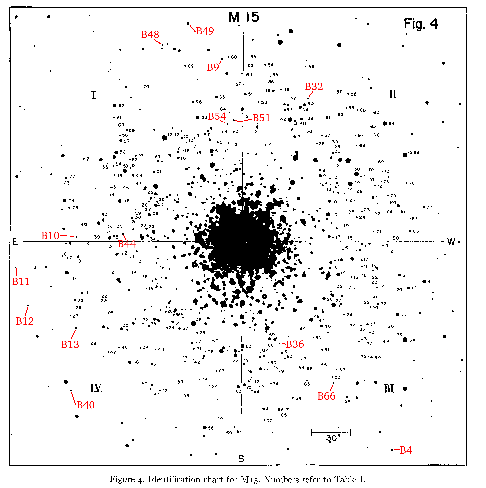
Compare this image with the map of M15 in the image file m15_arp1955.jpg.
This is a reproduction of a figure published in Color-magnitude diagrams for
seven globular clusters, by Halton Arp,
Astronomical Journal 60 317 (1955). While the article is an old one,
it still provides some of the best available data on the brighter stars of the
cluster.
This figure labels the individual stars so that you can look up their ``visible''
magnitudes. Although our CCD detector is
more sensitive to red light than to blue light, we can approximately compare
these photographically measured magnitudes to the unfiltered CCD images.
Later, for more precision, we
may take images in different colors and measure the color index of each
star as well as its magnitude.
Select a 100 second exposuredark-subtracted image of M15 and use the
Zoom->Invert Y selection so that north will be at the top. This will
help when you compare your image with the map.
Use the Scale->Parameters submenu and adjust the lower and upper limits
of the signal to show
every faint star. The center of the cluster will be saturated and completely
white on the screen, but you may adjust the contrast and bias using
the Scale->Scale Parameters submenu to make the faint stars clearly
visible.

The numbers on the figure refer to entries in the tables. (The stars marked with B are variable.) Notice that the reference map image of M15 is divided into four Roman Numeral sections and that each section has a list of numbered stars in the table. You may read the tables at the computer by using the command
gv m15_tables.ps
arp_m15_var.fits that you may display with ds9 for comparison with
the images from the telescope.

The visible magnitudes are called ![]() where the subscript is for ``photovisual''.
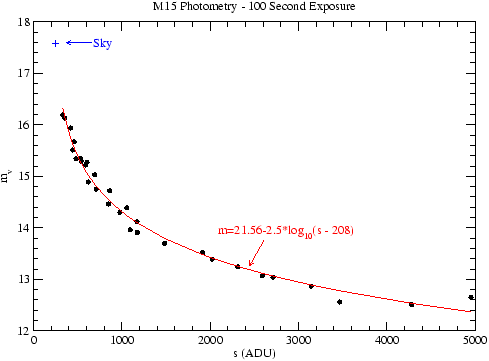
Find about 10 stars on the image including some that are very faint and others
that are very bright. The range of digital signals from these should span
from less than 500 at at the low end to more than 4000 at the high end.
Make a table listing the star identification, the photovisual
magnitudes (
where the subscript is for ``photovisual''.
Find about 10 stars on the image including some that are very faint and others
that are very bright. The range of digital signals from these should span
from less than 500 at at the low end to more than 4000 at the high end.
Make a table listing the star identification, the photovisual
magnitudes (![]() ) and the measured digital signal from the
CCD image (
) and the measured digital signal from the
CCD image (![]() ). Also include in your table a column with values of
). Also include in your table a column with values of
![]() . You will see why this is useful in just a moment.
Use the data in this table to plot graphs with
. You will see why this is useful in just a moment.
Use the data in this table to plot graphs with
![]() versus
versus ![]() and
and ![]() versus
versus ![]() . For this experiment you may do this by hand, but there is
powerful software available on these computers called grace or xmgr that is very useful
for scientific data analysis. If you want to try that and you are unfamiliar
with its use, ask for help.
. For this experiment you may do this by hand, but there is
powerful software available on these computers called grace or xmgr that is very useful
for scientific data analysis. If you want to try that and you are unfamiliar
with its use, ask for help.
You will notice in your graph that a larger magnitude means a smaller signal,
and also that the relationship is not a linear one.
Magnitudes (![]() ) arose historically from measurements made visually with the
unaided eye. In the present day quantitative form they are a
logarithmic scale of luminosity (
) arose historically from measurements made visually with the
unaided eye. In the present day quantitative form they are a
logarithmic scale of luminosity (![]() ) such that an increase of
) such that an increase of
![]() in
in ![]() results from a factor of
results from a factor of ![]() decrease in
decrease in ![]()
What magnitude corresponds to ![]() ?
?
Rewrite your solution in this form
An example of the relationship is shown in this figure, but it may differ from the values for your image.
What do you think the faintest star (highest magnitude) you could measure on this image would be? Why?
Some of the stars in M15 pulsate in brightness with periods from 0.30 to 1.44
days,and a average range from minimum to maximum of about 0.8 magnitudes.
Stars that fall in a particular class called RR Lyrae
stars (named after a prototype in Lyra) all have about the same physical
properties. The absolute magnitude (M) of a star is the magnitude it would
have if it were 10 parsecs, about 33 light years, from us. We know from
measurements of the statistical properties of the proper motion
of nearby RR Lyrae stars that their mean absolute
magnitude is about ![]() independent of their period of variability. The
mean magnitude of an RR Lyrae star, taken as the average of its minimum and
maximum magnitude, is also independent of its period.
If you know the absolute magnitude of a star, you
may use the relationship
independent of their period of variability. The
mean magnitude of an RR Lyrae star, taken as the average of its minimum and
maximum magnitude, is also independent of its period.
If you know the absolute magnitude of a star, you
may use the relationship
Which stars in M15 are variable? A sequence of images taken frequently over the course of a night would show them blinking, some from maximum to minimum to maximum again in about 3 hours. If we have such a set, use them to find several RR Lyrae stars. If not, several are marked on the map of M15 with the labels B ... for a catalog made by Solon Bailey in 1919.
Use variable stars you have identified, or a few marked with
B on the map.
What is the apparent magnitude of these stars?
If their average absolute magnitude is ![]() , what is the distance of M15
in parsecs?
, what is the distance of M15
in parsecs?