Special Relativity
Special Relativity: Space, Time, Motion, Mass and Light
Special Relativity gives new meaning to old ideas of time, space, motion, and mass. General Relativity adds acceleration and gravitation.

Special Relativity was conceived by Einstein in 1905 (he was only 26 years old) to explain a conflict between our concepts of light and of motion. His solution is based on two simple and seemingly contradictory postulates:
- The speed of light in a vacuum is constant, independent of the motion of its source, or its observer. (This was proved by Michelson–Morley experiment in 1887.)
- The laws of physics are the same for motion at a constant velocity as they would be for no motion at all.
(Bouncing a ball in a smoothly moving train is the same as it would be on the ground. Close the window shades while you are on an airplane, and you have no sensation of motion.)
Einstein introduced the revolutionary new idea that space and time are not rigid and absolute. He showed us that time, distance, and mass undergo changes that defy common sense as velocities approach the speed of light:
- Time measured by a moving clock runs slow.
- Distance measured while moving seems shortened.
- Mass of a moving object seems increased.
Moving time becomes warped, stretched out. A cosmic ray muon that would decay in a millionth of a second standing still, lives long enough to reach the ground. A precision clock placed in an airplane and flown around the world returns home reading slow. One second would become an eternity close to the speed of light.
As time expands, space shrinks. How would the cosmic ray muon make it all the way to the Earth's surface in its millionth of a second lifetime? It encounters a distance that is much less because it is moving so fast. This can be tested with a cloud chamber, by counting cosmic rays at the top of a mountain, and again at the bottom. To the muon it seems that the distance has contracted.
Mass and energy are equivalent -- remember the formula E=mc2? The faster something moves, the more energy it has, and the more mass it has. That's why matter cannot go at the speed of light! Its mass would be infinitely large, and it would take all the energy in the universe to get it up to that speed
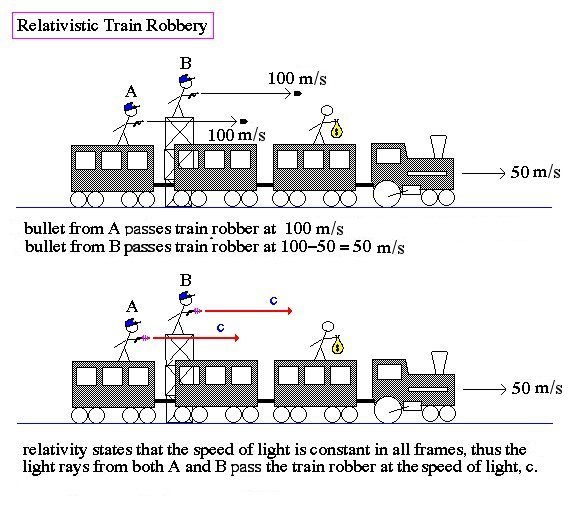
Example 1: A Relativistic Robbery
In the following scene of violence, the conductor on the train and the stationmaster on the tower both shoot at the train robber with similar weapons. Fortunately for the robber, neither are good shots so nobody gets hurt. At low speeds, the conductor on the train, who is not supposed to be carrying a concealed weapon in the first place, shoots at the hapless unarmed robber, and the bullet zips past at 100 m/s. He and the bandit are in the same "reference frame", both moving along together at a constant speed. The stationmaster's bullet from the tower zips by at only 100 m/s - 50 m/s = 50 m/s because of the trains motion. This is everyday, common sense, relativity. It's the kind of relativity that Galileo and Newton thought about.
But what happens if the defenders of the train are using "laser" guns, blasting photons at the speed of light. Now both photon blasts pass the robber at the same speed of light. Shouldn't those photons be zipping past at c (300,000,000 m/s) from the train, and c - 50m/s (300,000,000 m/s - 50 m/s) from the tower? In fact, all three participants will agree that the photon blasts are travelling at the speed of light.
Example 2: Receding Galaxies
Something familiar from astronomy are the receding clusters of galaxies. The wavelengths we measure are longer, the crests of the light waves are farther apart, for redshifted clusters speeding away from us. The light itself still comes to us at the usual speed of light, 300,000 km/s.

The most distant galaxy that has been found so far is IOK-1 with a redshift of 6.96 (as of September 2006).
The expansion of space causes the more distant galaxies to recede. The more distant and faster they recede, the slower time seems to be running on them. To calculate their velocity of recession we may no longer use z = v/c, but, when z is greater than 0.1, say 6 for example,
v = c ((1+z)2 - 1) / ((1+z)2 + 1)
v = c ((1+6)2 -1)/((1+6)2 +1)
v = c ((7)2 - 1)/((7)2 + 1)
v = c 48/50
v = 0.96 c
For z = 6, the velocity of recession is 96% of the speed of light. You may try this with any z, even z = 1000, the redshift of the cosmic background radiation.
Example 3: No Material Object Can Exceed the Speed of Light

As an object's speed approaches the speed of light from an observer's point of view, its mass appears to increase thereby making it more and more difficult to accelerate. The only things that could go at the speed of light are particles that could have no mass. These are the ones responsible for the fundamental forces: photons (light), W and Z bosons (weak force), gluons (strong force), and gravitons (gravity). However the W and Z that are seen in nature have gained some mass, and the graviton has not been observed. We are left with two examples: photons, which are everywhere, and gluons which require the biggest accelerators to create.
An example is an electron accelerated to the maximum energy possible at SLAC National Acceleratory Laboratory in California. In the laboratory its energy is about 50 billion "electron volts", about 4 billion times more energy than an electrons that come out of your car's battery. With that much energy, the electrons travel at 0.999999995 times the speed of light, and they have increased in mass by nearly 100,000 times. That makes the tiny electron coming out of the SLAC accelerator almost 50 times the mass of a proton at rest. Collide one of these with its anti-particle, the positron, and gluons will appear.
The faster the object goes, the more slowly its "clock" seems to run. That's why a particle travelling at the speed of light can never change. Photons cannot decay. The cosmic background radiation photons have been travelling freely through the universe unchanged for 13 billion years.
According to Special Relativity material objects cannot pass one another faster than the speed of light. Only at the beginning of the universe did anything travel faster than the speed of light ... Space!
Addition of Speeds

Velocities or speeds do not simply "add" the way that Galileo and Newton thought they should. For example if the first stage of a rocket were moving at 2/3 the speed of light relative to an observer, and the rocket fired off its next stage at 2/3 of the speed of light relative to the rocket, the next stage still does not exceed the speed of light relative to the observer. The observer would see that stage travel with a speed of 12/13 the speed of light.
Again, the math for this is not hard. If va and vb are the two velocities, then the total is
vtotal = (va + vb) / ( 1 + (va vb /c2))
If you experiment with this formula a little you'll see that the total is always less than c, for any two velocities less than c. A light beam seen from a fast moving rocket will seem to be traveling at the same speed of light as always.
Time Dilation: Twin Paradox
For two observers moving past one another, each perceives that the others time is moving more slowly. It does seem paradoxical, but we've proven it by making very precise measurements of time with clocks moving at modest speeds, and by measuring the decay of fundamental particles as they move at nearly the speed of light. There is a good video that explains how time dilation occurs.

The twin paradox concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that his or her twin sibling has aged more.
Suppose you were to travel at nearly the speed of light to the star Sirius, 8 light years away. To you the journey would seem almost instantaneous because the distance to Sirius will appear shortened. By how much? If the spaceship is travelling at 98% of the speed of light, the 8 light years would be only 0.2 light years. The trip would take about 2.4 months. Make a quick stop, pick up some souvenirs, and return home 2.4 months later. You're back home in less than half a year, having made a journey of 16 light years round trip.
To your friends on Earth, you traveled at nearly the speed of light, and took 8 years of their time to make the trip out, and another 8 years to get back. You've been gone for 16 years! Your friends, perhaps 30 years old when you left, are now 46. The fun is in the time dilation . You're only 30 plus 5 months.
As a space farer, you saw the distance to Sirius contracted, and the trip was fast. For your friends left on Earth to age, they saw your "clock" running very slow. To them, your trip took 16 years and your clock ran almost 32 times slower than theirs. The faster you go, the slower your clock would seem to run. That's time dilation. Both those who stay, and those who travel, would agree.
The "paradox" comes into view if you think about what you, as a traveller, would see for your friend's clock back on Earth. As you look at them it, receding from you at nearly the speed of light, you'd see their clock running slowly. How is it that when you arrive back on Earth, they are older and you are not (by much)?
The answer to this lies not in Special Relativity, which applies only when speeds are steady and not changing, but in General Relativity. That theory tells us what happens when there is acceleration, or gravity. Let's just say here that there is a real difference between the experience that you had travelling to Sirius, and your friends had staying on Earth. You accelerated up to light speed compared to the rest of the Universe, and then slowed down again, twice.
Relativity of Simultaneity
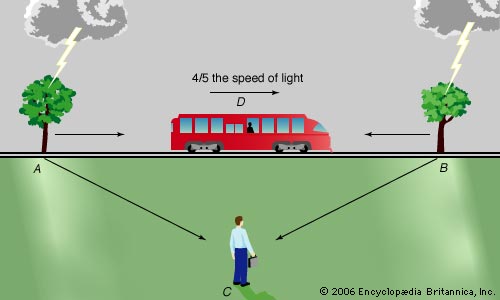
The observer at C thinks that the two lightning flashes are simultaneous, but the observer in the train will see them at different times.
It is fairly simple to understand why time itself is relative by thinking about simultaneus events, and there is a good video illustrating this. Two events happening in two different locations that occur simultaneously in the reference frame of one inertial observer, will occur non-simultaneously in the reference frame of another observer moving at a constant speed. This is called lack of absolute simultaneity.
So it is impossible to have an absolute time describing when an event happens. In fact, time and space are mixed and we must describe how both transform because of the motions of the observer. That's Einstein's big discovery, and its why we talk about "spacetime".
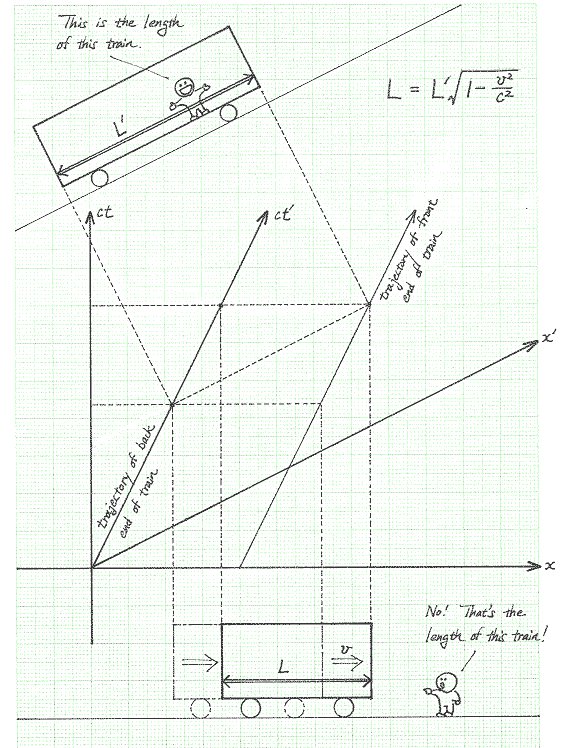
Lorentz Contraction
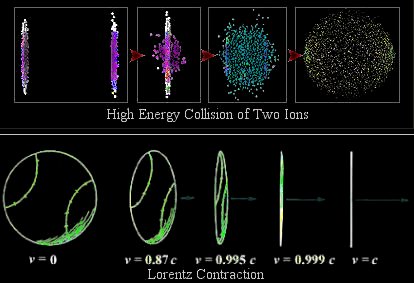
Protons or other ions with charge appear to flatten as they near the speed of light. To a physicist in the laboratory, they would appear to be pancakes before they smash together in a collider.
The dimensions (length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer. (This leads to the ladder paradox involving a long ladder traveling near the speed of light, caught in a small garage).
The Math of Special Relativity
Time measured by a moving clock seems to run slow:
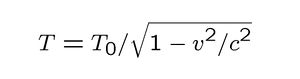
T0 is how long a tick of the clock lasts when it is not moving. T will be infinitely long for a clock moving at the speed of light.
Distances seems to contract when we move:
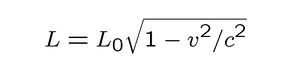
At nearly the speed of light, a trip to Sirius would be short indeed.
A galaxy at the edge of the universe, moving away at nearly the speed of light, has a red shift z:
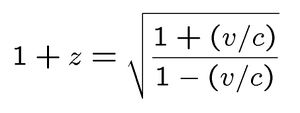
For a galaxy receding at nearly the speed of light , z will be very large.
Lorentz Transformations
The consequences of Special Relativity can be described by the Lorentz transformations. Lorentz transformation matrices for Special Relativity have 4 dimensions, 3 dimensions of space and one of time. The transformations describe how space and time are transformed by motion.
While we won't go into the math, the Lorentz transformation for 4-dimensional spacetime look like this.
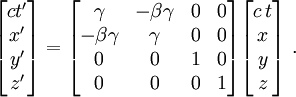
Space along the direction of motion and time are connected, transformed, into one another.
Mass Energy Equivalence

E=mc2
To grasp the huge amount of energy the early Universe took to create matter, consider the small amount of matter it took to create this thermonuclear explosion. The equivalent of 1 megaton of TNT uses up only about about 46 grams of matter. The energy from the Sun that warms the Earth comes from the conversion of a tiny part of the mass of the hydrogen atom into energy.
The principle of mass-energy equivalence was developed by considering the effects of relativity on the motions of particles with mass. It was found that a fast moving object would have more mass than a slow moving one. What Newton had thought of as energy of motion was, in this new view, an increase in the mass of the object to make mc2 larger. Similarly, the mass of an object can be increased by adding kinetic energy, that is, by being accelerated. At the Large Hadron Collider when particles are accelerated their mass increases.
Tests For Special Relativity
For anyone wishing to pursue Special Relativity further, there have been a number of experiments conducted to test special relativity , especially some years ago when its results seemed so extreme. These include:
- Kaufmann-Bucherer-Neumann experiments – electron deflection in approximate agreement with Lorentz-Einstein prediction.
- Fizeau experiment – speed of light in moving media in accordance with relativistic velocity addition
- Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Rossi-Hall experiment – relativistic effects on a fast-moving particle's half-life
- Experiments to test emitter theory demonstrated that the speed of light is independent of the speed of the emitter.
- Hammar experiment – no "aether flow obstruction"
In addition, particle accelerators routinely accelerate and measure the properties of particles moving at near the speed of light, where their behavior is completely consistent with relativity theory and inconsistent with the earlier Newtonian mechanics. These machines would not work if they were not engineered according to relativistic principles.
Perhaps most convincingly, the "Global Positioning System" (GPS) receivers that are so common today use carefully timed signals from satellites in orbit around Earth. It is the difference in arrival time of these signals that enables a unit to calculate its location on Earth to a precision of less than a meter. Those satellites are in motion, and the signals and times are subject to the laws of Special Relativity. That they work is a testamonial to the power of the "top down" logic that Einstein applied to his analysis of the natural world. He was thinking about clocks, trains, and light, not about the practical use of his ideas in the GPS system.
General Relativity
Special relativity was developed to explain a conflict between the theories of light and of motion as understood in 1905. It did not take into account acceleration, or gravity, two neccessary components of a complete theory of "mechanics". It took Einstein a few more years to make sense of it, and supply us with the tools we need to complete our description of the Universe. General Relativity is the theory of how space and time are connected to mass, energy, and motion. In the next page we will briefly look at what this means in the extreme case of a black hole, an object so massive that it cuts itself off from the rest of the universe.